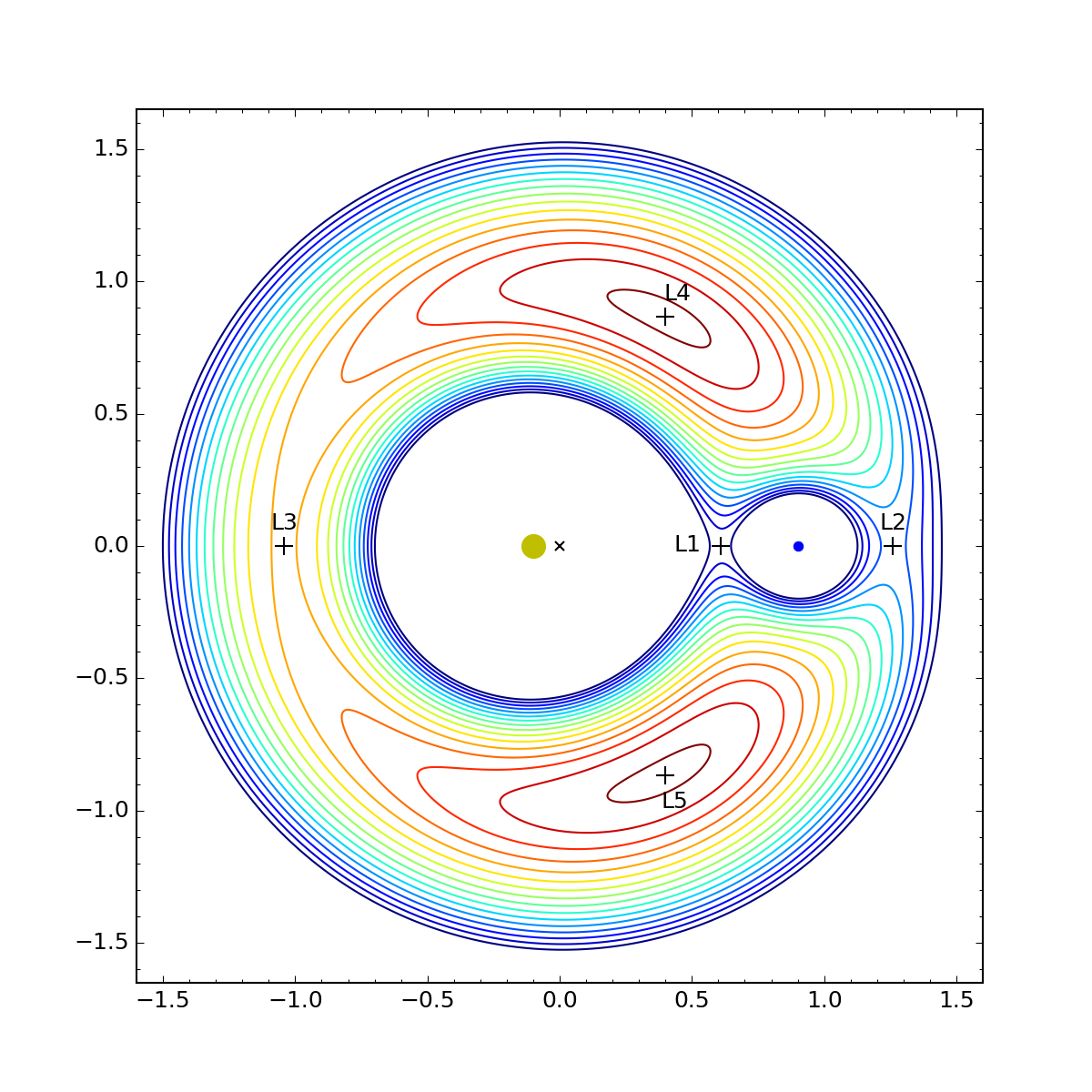
Celestial Mechanics: Lagrange Points
A Lagrange Point is a position in space where the gravitational forces of a two body system, such as the Earth-Sun system, is equal to the centrifugal force felt by a (much much smaller) third body. These are points of equilibrium where an object can be kept at a relative hault without the need for any orbital correction. The earth-sun Lagrange points (like other 2 body systems), has 5 Lagrange points, labeled in the diagram.
This project was focused on finding both analytical and numerical solutions to find these Lagrange points. For L1, L2, and L3, we can obtain these by using appropriate Taylor expansions. We can also check these against numerical solutions found through root-finding methods such as Newton-Raphson. For the L4 and L5 points, we can use the secant approach with finite differences.
You can take a look at my analytical work →HERE←
and the code on Github →HERE←
This project was focused on finding both analytical and numerical solutions to find these Lagrange points. For L1, L2, and L3, we can obtain these by using appropriate Taylor expansions. We can also check these against numerical solutions found through root-finding methods such as Newton-Raphson. For the L4 and L5 points, we can use the secant approach with finite differences.
You can take a look at my analytical work →HERE←
and the code on Github →HERE←